Solutions
 KM#12: Age of the Earth (Level 4)
KM#12: Age of the Earth (Level 4)
Mathematical Content: Basic algebra; exponential equations; logarithms; linear regression.
Part 1: Worked solutions are provided in modules at the “clicks” and following the answers for parts I and II below:
Answers Part I
Question 1. What is the value of the decay constant for rubidium-strontium?
λ = 1.42 x10-5
Question 2. Suppose that in an isotope system, the parent decays into the daughter, and there was no daughter atoms present initially. What is the ratio of daughter atoms to parent atoms at time t?
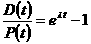
Question 3. What is the age of the gabbro from Electra Lake?
The gabbro is, approximately, 1,429 million years old.
Solution for Part 2
Question. How old is the Earth?
In order to answer this question, you can repeat the procedure given in the dating of the gabbro; specifically:
- Plot the data on an (x, y)-axis system to create the isochron diagram
- Use linear regression to find the slope of the line of best fit
- Set the slope equal to
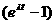
- Solve for t.
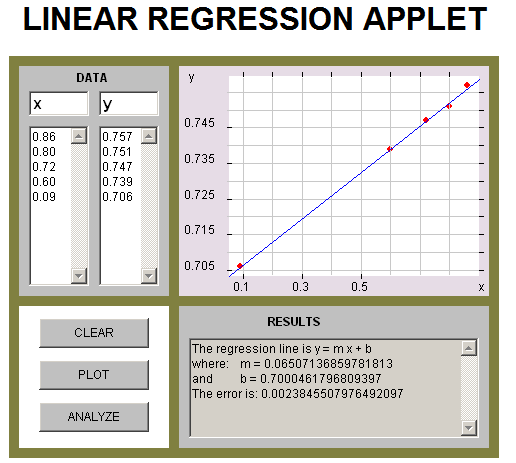
The slope is m = 0.065 (and 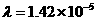 ).
).
Solve
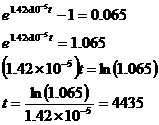
The age is approximately 4435 million years, that is, 4.435 billion years.
Worked Solutions for Part I
Solution to Question 1. Use the basic decay equation P(t) = P0e-λt. When
t = half-life for Rb-Sr = 4.88 x 104 million years,
then the initial number of atoms is reduced by half (from 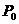 to
to 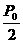 ) , so denoting half-life by h, set t = h and solve
) , so denoting half-life by h, set t = h and solve 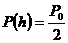 for l.
for l.
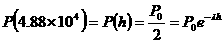 ,
,
So now we solve 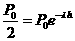 for λ, with h = 4.88 x 104.
for λ, with h = 4.88 x 104.
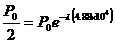
Cancel P0 from each side, then take the natural logarithm of both sides,
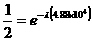
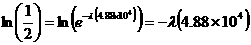
But
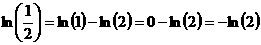
so
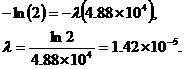 .
.
We have found the decay constant λ = 1.42 x10-5 for the Rb-Sr system
.
Solution to Question 2. First, solve the basic decay equation for P0,
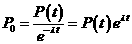
Now let D(t) denote the number of daughter atoms at time t. The number of daughter atoms at time t is equal to the number of parent atoms present initially minus the number of parent atoms at time t, so
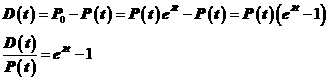
Solution to Question 3. Solve the equation
0.0205 = eλt – 1,
with λ = decay constant for Rb-Sr = 1.42 x10-5, for t.
We present two solutions, one is algebraic, the other is graphic using the plot-solve applet.
Algebraic solution.
Solve 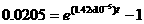
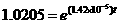
Take the natural logarithm of both sides and then solve for t,
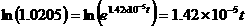
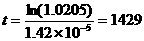 .
.
The gabbro is, approximately, 1,429 million years old.
Graphical solution.
To solve the equation 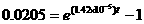 , graph each side and determine the point of intersection.
, graph each side and determine the point of intersection.
(The graph shown below is copied from the Earth Math or Kéyah Math website Plot/Solve applet.)
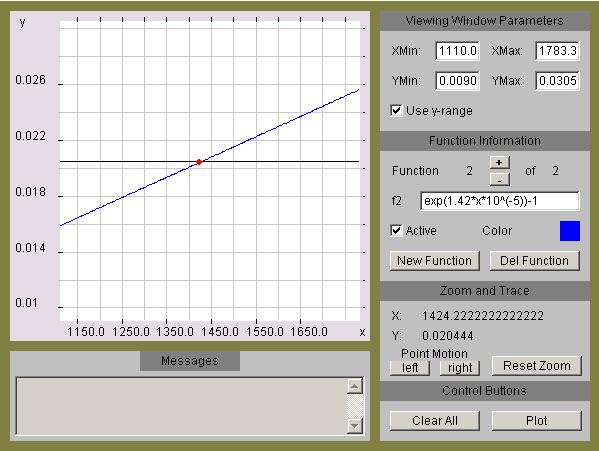
The gabbro is, approximately, 1,429 million years old.