Solutions
KM#8: Age of the Earth (Level 2+)
Mathematical Content: Basic algebra; exponential equations; logarithms.
Question 1: What is the age of the gabbro from Electra Lake?
(Hint: Equate the value for m to the slope in the decay equation and solve for t.)
Solve the equation
0.0205 = eλt – 1, with λ = decay constant for Rb-Sr = 1.42 x10-5, for t.
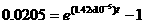
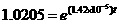
Take the natural logarithm of both sides and then solve for t,
.
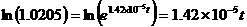
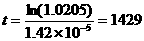The gabbro is, approximately, 1,429 million years old.
Question 2: How old is the Earth? In order to answer this question, you can repeat the procedure given in the dating of the gabbro; specifically:
- Plot the data on an (x, y)-axis system to create the isochron diagram
- Use linear regression to find the slope of the line of best fit
- Set the slope equal to
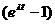
- Solve for t.
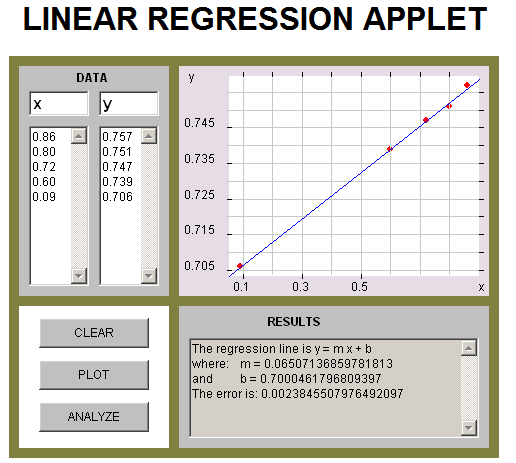
The slope is m = 0.065 (and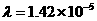 
).
Solve
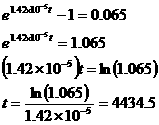
The age is approximately 4435 million years, that is, 4.435 billion years.