Age of the Universe: Exercises

The objectives and assumptions of this study are listed below. These will appear in each of the Kéyah Math Studies.

Objectives
To determine:
1. a linear model for distance of a galaxy from the earth against the velocity of recession;
2. an estimate for the age of the universe.

Assumption
The relation between distance and velocity is linear.

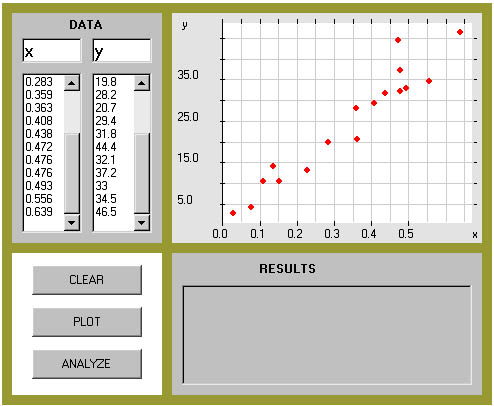
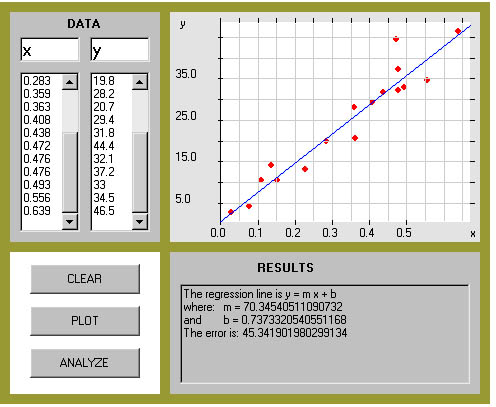
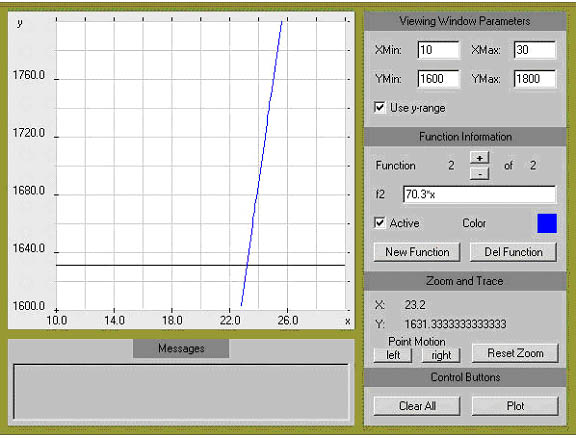
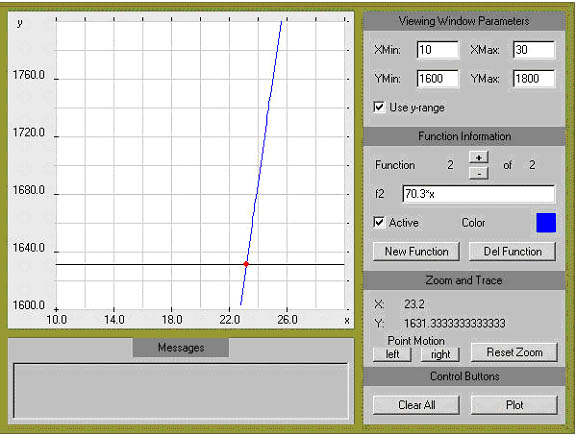
d(x103)	v(x103)	Constructing the Hubble Diagram The data points to the left are taken from a plot of redshift z of receding galaxies against their distance d from Earth (Galaxies and Cosmology, Jones and Lambourne, page 243) with the second row indicating redshift x velocity of light = velocity of recession of galaxy = v The numbers in the distance column give distance d of the galaxy from Earth in Megaparsecs x 103 (Mpc); the velocity is kilometer per sec x 103. So, for example, a galaxy which is 0.028 x 103 Mpc from Earth is receding at a velocity of 2.7 x 103 km/sec. Linear Models In this part, you will find a linear function to express the relationship between distance and velocity. Specifically you will: * express velocity as a function of distance from the earth, * find the Hubble constant, and * determine how fast the Whirlpool Galaxy is receding from us. For this demonstration module, instructions are provided in italics and solutions are in blue italics.
0.028	2.7
0.076	4.2
0.108	10.5
0.136	14.1
0.153	10.5
0.226	13.2
0.283	19.8
0.359	28.2
0.363	20.7
0.408	29.4
0.438	31.8
0.472	44.4
0.476	32.1
0.476	37.2
0.493	33
0.556	34.5
0.639	46.5

Problem Set (Round off to three decimal places for this work.)

The applets needed to complete this problem are provided in the text for this Introductory module. Usually, you will need to follow these steps. (You may choose to use your graphing calculator to do this work-ask your instructor.)

* Click "linear regression" (since we are looking for a linear function).

The linear regression applet will open in a separate screen.

Question 1: Plot the points corresponding to the data in Table 1. The first coordinate is distance from the earth; denote this by d (units are 103 Mpc). The second coordinate is velocity of recession of galaxy, units 103 km/sec. You can copy each column from the table and paste it into the appropriate column of the applet.

Enter the data provided in Table 1into the columns on the applet screen; enter the d value in the "x" column, then enter the v value in the "y" column. You can copy each column from the table and paste it into the appropriate column of the applet.

Click "Plot", you should see the screen below.

 

Question 2: Now find the line of best fit. (The resulting graph is called a Hubble Diagram.)

Click "analyze" on the applet containing the plotted data and see the screen as shown.

The equation of the line is shown in lower right window of the applet screen:
y = 70.345x + 0.737.

Question 3: What is the slope of this line? What are the units?

The slope is indicated by the constant m, it represents the change in y divided by the change in x. The units for the numerator are the units for velocity, 10³ km/sec; the units for the denominator are units for distance, in this case 10³ Mpc; thus the units for the slope are (km/sec)/Mpc.
m = 70.345 ( km/sec)/Mpc.

Your answer is the Hubble constant, denoted by H₀. Here's what it means: if a galaxy is 10 Mpc away from us, it is receding at the rate of 10 x 70.345 km/sec = 703.45 km/sec; if a galaxy is 15 Mpc away, it is receding at the rate of 15 x 70.345 km/sec = 10⁵5.175km/sec; etc.

Question 4: The Whirlpool Galaxy is approximately 30 x 106 light years away from us. (One light year is the distance that light travels in one year.) How fast is it receding from us? We need to use the same units for all measurements, so converting 30 x 106 light years to Mpc, we get 9.2 Mpc.

Now use the Hubble constant to answer the question.

Information: We can use the Hubble constant to approximate the age of the universe. The modified equation from #1 (ignoring the very small constant, assuming that when d = 0, then v = 0, and rounding the Hubble Constant to one decimal place), v = 70.3d, is known as Hubble's Law.

 

Question 5: A Black Hole, Perseus A, has been detected traveling away from us at the rate of 1631 km/s. How far away is it?

This could actually be solved easily by dividing 1631 by 70.3, however we will use the Plot-Solve Applet to show how it can solve equations. The equation we need to solve is

1631 = 70.3d,

for the distance d.

Click "Tool Chest" on the left menu, and then click "Plot-Solve." You'll see the screen below.

Now click "New Function" and type in the left side of the equation, 1631; then click "Plot."

Next, click "New Function" and type in the right side of the equation (remember to use * for multiplication, and use x for d), 70.3*x; then click "Plot again".

The screen at this point doesn't look very interesting. The reason is that the graph of y = 1631 is outside the range of the screen, so you'll need to change the y-range. Enter 1600 for "YMin" and 1800 for "YMax"; this range includes 1631, which is what we want to see.

We also want to see the solution, so you'll need to change the x-range also: let's guess and enter 10 for "XMin" and 30 for "XMax."

Now, click "Plot" again. You should see the screen shown below. The solution to our equation is the x-coordinate of the intersection of the two graphs.

Place the point of the arrow on your cursor right on the intersection of the two graphs and click "Plot." The x-coordinate can be read in the window to the right of the screen, you should see

x = 23.2.

So, the black hole is 23.2 Mpc away from Earth.

 

Question 6: Recall the well-known formula for distance, distance = (rate of speed) x (time traveled), or d = vt, and substitute this into the Hubble Law for d. Simplify the result and solve for time, t.

v = 70.3d
v = 70.3(vt)

Cancel the v from both sides to get

1 = 70.3t

Solve for t to get

t = 1/70.3

In order to keep the same units and express the age of the universe in years, the Hubble constant, H₀ = 70.3 km/s (per Mpc), expressed in Mpc/yr (per Mpc) is 72.5 x 10^-12 Mpc/yr (per Mpc).

Question 6: Using this value for the Hubble constant (replace 70.3) and the answer to Question 6, compute t. This answer is a very good approximation to the current age of the universe.

t = 1/(72.5 x 10^-12) = 13.8 x 10⁹ years, or 13.8 billion years
(Note the units here: the Mpc's cancel leaving only years.)

Return to the home page

 

• Arizona Board of Regents ± Copyright Statement ± Acceptable Use Policy