Arizona State University School of Earth and Space Exploration

 

Demonstration of Math Applets

Instructions and a detailed help menu are provided with each applet. This demonstration module illustrates the use of the two of them: the Java Math Pad Applet and the Plot-Solve Applet.


Java Math Pad Applet
This applet allows the user to evaluate mathematical expressions. A mathematical expression is made of numbers, variables, built-in and user defined functions together with operations. For more information on the use of this applet, click on the scroll down menu under "Help Topics". The following examples will illustrate some of the features of the applet.


Example 1 Entering and Evaluating Mathematical Expressions

Evaluate the expression 3ab - 4c3 when a = -2, b = 3, and c = -5.

Solution

Begin by assigning values to the variables. On the Math Pad screen,

 

type a = -2, then press enter;

type b = 3, then press enter;

type c = -5, then press enter;



Next we type the expression using * to indicate multiplication and ^ for exponents and press enter. Java Math Pad will return the numerical value of our expression. See Figure 1.


img

Example 2 Defining and Evaluating Functions


Evaluate the function f(x) = -3x2 + 17x - 33 when x = -2.4

Solution

Click on the Clear button to clear the Java Math Pad screen. Then type f(x)=-3*x^2+17*x-33 and press enter to define the function. Now type f(-2.4) and enter. Java Math Pad will return the value of the function. See Figure 2.

 

img

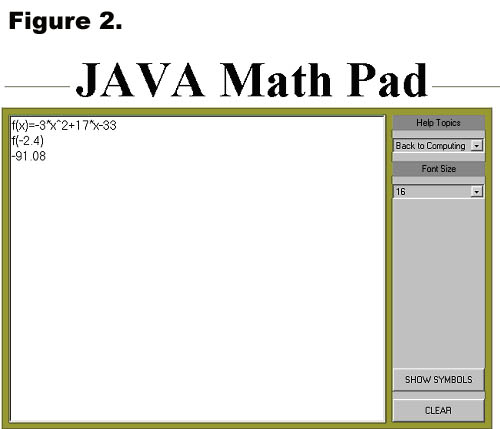
The function f(x) will be stored in Math Pad's memory until clear it. So, you can evaluate the function for as many different values of x as you desire. To clear a defined function from Math Pad's memory type "clear function name". For example, to clear the function f(x) that we just defined, type, "clear f ". You can also simply define a new function named f.


Example 3 Evaluating Trigonometric Functions


Find the value of each of the following trigonometric expressions.
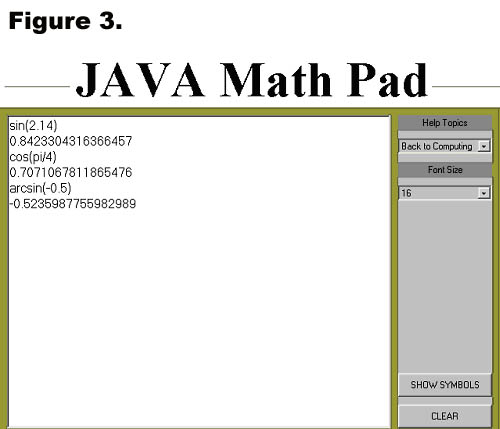
(a) sin(2.14)
(b) cos (π / 4)
(c) arcsin(-0.5)


Solution

The trigonometric and inverse trigonometric functions are built-in functions in Java Math Pad. In the case of the sine and cosine functions, the argument must be a number expressed in radians and must be enclosed in parenthesis. For the inverse sin, the argument should be a number between -1 and 1 and should also be enclosed in parenthesis; Math Pad will give the answer in radians. See Figure 3. For more information about the built-in functions, go to "built-in functions" in Java Math Pad's help menu.

img


Example 4 Combining Functions to Form a New Function


Given the functions f(x) = 2x + 5, g(x) = 3x2 + 2, and h(x) = √x-1 evaluate each of the following:
(a) f (-2) + g(-2)
(b) f(1) / g(1)
(c) h (f(6))


Solution


Click the Clear button to clear the Math Pad screen. Next define the three functions. Use sqrt to denote the square root. Type f(x)=2*x+5 and press enter, then type g(x)=3x^2+2 and press enter, and finally type h(x)=sqrt(x-1) and press enter once again.


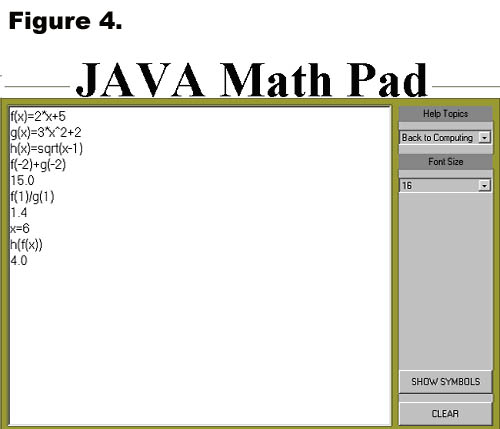
(a) Simply type f(-2)+g(-2) and press enter. Math Pad will return the numerical value.
(b) For this problem, type f(1)/g(1) and press enter.
(c) To evaluate the composite function h(f(x)) when x = 6, you must first assign the value 6 to the variable x. To do this type x = 6 and press enter. Then type h(f(x)) and press enter. See Figure 4.

 

 img

Plot-Solve Applet


The purpose of this applet is to plot functions. It can plot up to 10 different functions at the same time. It can also be used to solve equations numerically. This demo includes Instructions for using the applet and examples that will illustrate some of the features.


1. The Viewing Window Parameters area is used to set the area of the graph the user wishes to see. Use it as follows:

2. The Function Information area is where the functions to be plotted are entered. Use this area as follows:

  • To enter a new function, always press the New Function button. Then, enter the expression defining the function. The syntax is similar to the syntax used in the Java Math Engine. For example, to defines the sine function, you would type in sin(x). Make sure you use x for the variable in your definition.
  • A maximum of 10 functions can be defined at the same time.
  • Checking Active means the function will show on the graph. Unselecting it means the function will not show.
  • Use the + and - buttons to scroll through the list of defined functions.
  • Each defined function has a different color assigned to it. The selection is automatic.
  • When a function is defined, it is automatically assigned a name of the form fi where i is a number which starts at 1 and is incremented every time a new function is defined. The name a function will be saved under appears to the left of the field where it is defined.
  • Once a function is defined, its name can be used in the definition of other functions. For example, if two functions have been defined, the definition of function 3 could be f1(x)+x*f2(x) Note that we use f1(x) and not just f1.
  • The functions defined will plot only after Plot has been pressed.
  • Del Function will delete the function currently showing. When deleting a function, make sure that it is not used in the definition of another function. An error would occur in this case. For example, if f2(x) = x + f1(x) and f1 is deleted, then the definition of f2 contains an unknown symbol, f1.

3. The Zoom and Trace area is where zooming and tracing take place. Use this area as follows:

  • To zoom in, picture in your mind the rectangular region you would like to zoom in. Left click on one of the corners of this imaginary region. While holding the mouse button down, move it to the opposite corner, then release it. As you move the mouse, a rectangle will be drawn to help you visualize the region. Once the mouse button is released, the graph will redraw, XMin, XMax, YMin, YMax will be updated.
  • To go back to the original view (XMin = -10, XMax = 10, YMin = -10, YMax = 10), press Reset Zoom.
  • To trace, simply single left click in the graph area. A point will be generated by taking the x-coordinate of the point where you clicked and the y-coordinate on the function currently showing.
  • To move the point, use the Right or Left buttons. The point will move on the function currently showing. By selecting a different function, you can select which function you want your point to follow.
  • The coordinates of the point will be displayed under X: and Y:.

4. The Control Buttons area contains buttons which have a global effect for the applet.

  • The Clear All button erases all the function definitions.
  • The Plot button is used to update the plot area after changes in the other areas have been made.

5. The Messages area is where the applet communicates with the user. Error messages as well as user information is displayed there. Errors are displayed in red, while information is displayed in black.

Example 1

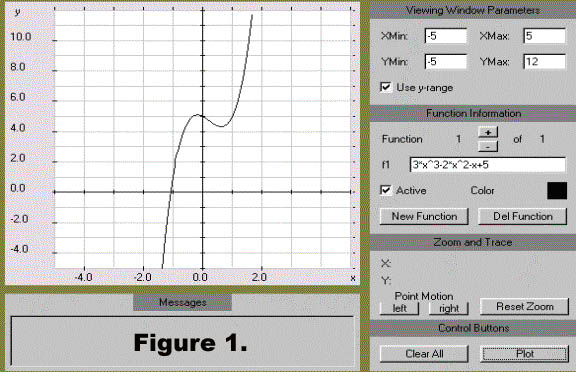
Graph the function f(x) = 3x3 - 2x2 + x + 5.


Solution

Step 1) On the Plot-solve applet, click the New Function button and type the expression for the function (do not type f(x)=) using * to indicate multiplication and ^ to indicate exponents, just as in the Java Math Pad applet.

Step 2) Set the viewing window. The default window is x-min -10, x-max 10,
y-min -10, y-max 10. You can change these values to give the best view of the function. In general, you can either specify the y-min and y-max or you can let the applet choose appropriate y-values for the function. If you wish to specify the y-min and y-max, "Use y-Range" must be checked. For this example, set the following values:
x-min -5, x-max 5, y-min -5, y-max 12.

Step 3) Click the Plot button.

Figure 1 below shows the graph.

img

Example 2 :

 

Solve the equation x = x3 + 1 graphically.

Solution

Begin by graphing both the left side and the right side of the equation on the same coordinate axes. To do this, click the New Function button and enter x. Next click New Function again and enter x^3+1. Click the Plot button. The resulting graph is shown in Figure 2. Notice that the default window, x-min -10, x-max 10, y-min -10, y-max 10 gives a good view of the graphs and their point of intersection.

img

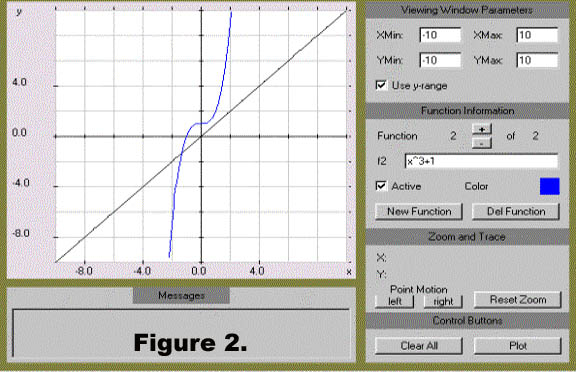
The graph in Figure 2 shows one point of intersection. The x-coordinates of this point is the solution to the equation. Follow the steps outlined below to estimate this solution.

Step 1) Place the cursor on the point of intersection and click the left mouse button. The coordinates of the point will appear in the Zoom and Trace portion of the applet. See Figure 3.

 

img

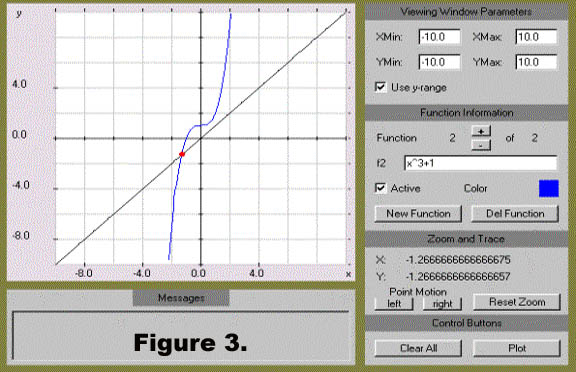
Step 2) Figure 3 shows that the x-value of the point is approximately -1.27. You can get a better estimate of this value by zooming in on the portion of the graph containing that point. To zoom-in on the graph, place the cursor on the graph near the point, but a little to the left and above it; then hold the left mouse button down and drag it to the right and down to form a "box" around the point of intersection. When you are satisfied with the "box", let go of the mouse button and the graph will be redrawn in that viewing window. See Figure 4.

img

Step 3) Notice that the close-up view shows that we were not actually at the point of intersection. Now move the point closer to the actual point of intersection using the left (or right) button under Point Motion. See Figure 5.

img

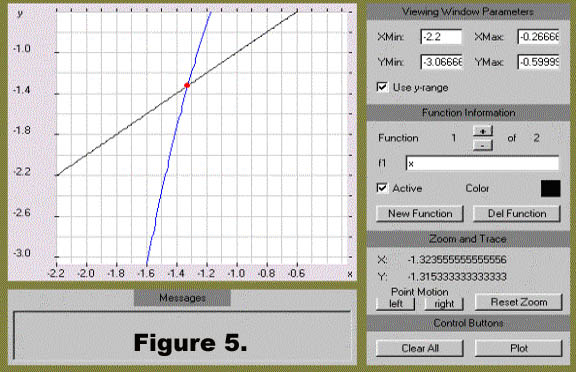
Just as before, the coordinates of the point are displayed by the applet. You can see that a good estimate for the solution to this equation is x = -1.32. You can repeat this procedure as often as necessary to get closer and closer estimates for the point of intersection.

This material is based upon work supported by the National Science Foundation under Grant GEO-0355224. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.