Keyah Math Study 6, Level 2
Mathematical Content : Equations of lines
 Location of the Epicenter of an Earthquake:
Location of the Epicenter of an Earthquake:
This is a study illustrating how earthquakes are located using data received at seismic stations. In particular, a 3.1 magnitude earthquake is used in this study. You will learn how geologists found out where it occurred.
Warm-up Steps
1. Do you know of any recent earthquakes near where you live?
2. If so, was any damage done?
3. Where have some earthquakes that you know about occurred?
4. How do you think that scientist know where an earthquake happened?
5. Why is it important to know where an earthquake occurred?
Introduction
An earthquake occurs when rocks in the crust move. This movement releases energy that is transmitted outward as seismic waves. Seismic stations have instruments that can sense and record seismic waves, even those from earthquakes that occur thousands of miles away from the station. Earthquakes generate several different types of seismic waves, and these waves each travel at different speeds through rock. The fastest waves (traveling at about 6 km/sec through most crustal rocks) are the first to arrive at seismic stations and are called primary (P) waves. The next fastest waves travel at about 3.5 km/sec, so they arrive at seismic stations later and have been termed secondary (S) waves. The farther these waves travel away from the source of the earthquake, the more the P waves will outpace the S waves.
The epicenter of an earthquake is a virtual point on the surface that is located directly above the source of the earthquake. The farther a given seismic station is from an epicenter, the longer the time interval between the arrival of the P waves and the arrival of the S waves. This time interval can be expressed mathematically as a function of the distance from the epicenter and the speeds of the P and S waves through rock. If we know what those two speeds are, and measure the time interval between the P and S arrivals at the seismic station, we can easily calculate how far the epicenter was from that seismic station.
The sequence of problems below will show you how this is done.
Using math to find the epicenter of an earthquake
Notation tp = number of seconds a P wave travels after the instant of the earthquake; ts = number of seconds a S wave travels after the instant of the earthquake; dp = distance (in km) P waves have traveled in tp seconds; and ds = distance (in km) S waves have traveled in ts seconds |
Step 1: Write an equation that shows how far each type of wave traveled after t seconds? Hint: Use the well-known formula, distance = rate x time, to write the two equations that express distance traveled by the waves in terms of lapsed time. Your answer should be written in the form dp = mptp, and ds = msts, where mp and ms are the slopes of the lines. |
Step 2: A) Solve each of the two equations from Step 1 for times, ts and tp. Since the distance is the same for each wave, denote this by D (= dp = ds). B) Take the difference of the results from Part A; be sure your answer is positive. Denote this difference by the variable U. C) What does your answer to Part B represent? D) Solve the equation from Part B for distance D. |
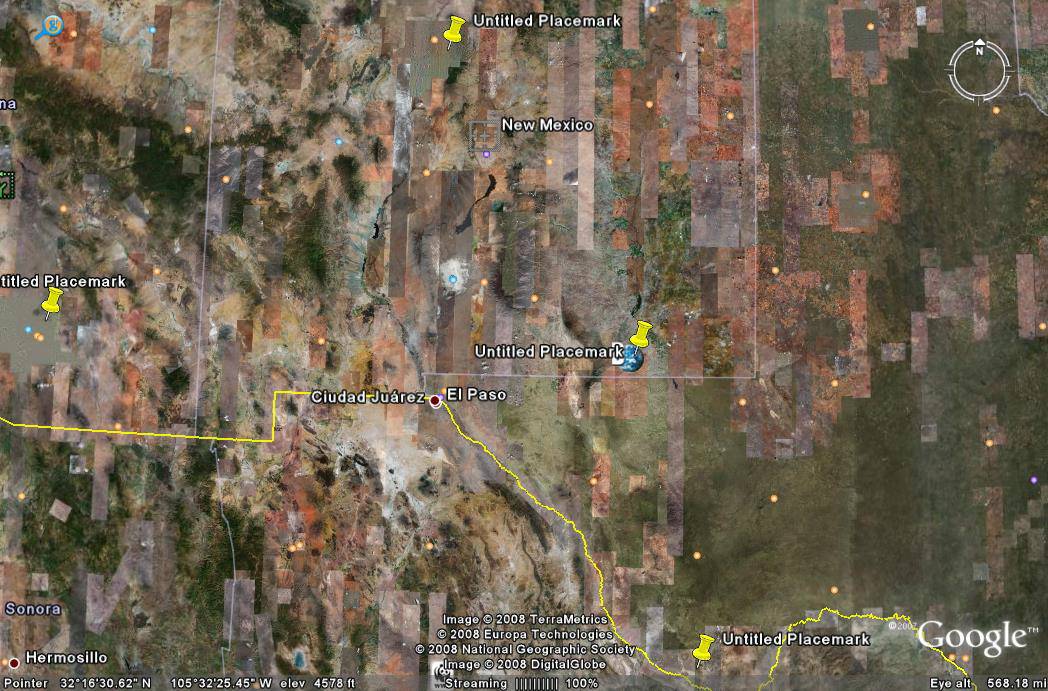
The table below shows four seismic stations near New Mexico (represented by 3- and 4-letter codes) with latitude and longitude coordinates given in columns 2 and 3. Columns 4 and 5 indicate the times that P and S waves were received at the stations. The last three blank columns are for arrival time of P- and S-waves differences U, distances D from the stations to the epicenter of the earthquake, and scaled down distances for the map shown below.
Station |
Arrival Time |
Arrival Time |
Time Diff U |
Dist to Epicenter D |
Scaled Distance for Map |
1. TUC |
3:31:25 |
3:31:54 |
|
|
|
2. ANMO |
3:31:28 |
3:32:00 |
|
|
|
3. GDL2 |
3:31:45 |
3:32:29 |
|
|
|
4. LTX |
3:32:22 |
3:33:32 |
|
|
|
Step 3: A) From the data given in the table above, compute the time differences in seconds that P and S waves were received at the stations. Complete the column for U in the table. B) Use your answers to Part A and the equation from Step 2B to find the distances from the stations to the epicenter of the earthquake to fill in the column for D. |
The distances you found in Step 3 can be used to find the epicenter of an earthquake. You know how far away the epicenter is from any one station but you don’t know what direction. For example, if the epicenter is 1000 km away from the seismic station, you know it must be somewhere on the circle centered at the seismic station with radius 1000 km.
The map on the next page is to be used to locate the epicenter. First, print this map.
Step 4. This a Google Earth map. The four markers locate the four stations listed in the table. From the latitude and longitude coordinates in the table, locate and identify each station. |
Step 5. Next, you will need to figure out the scale on the map. A) Measure, in inches, the east-west distance on the map along the southern border of New Mexico from Texas to Arizona. The real distance between these locations is 565.56 kilometers (Google Earth). B) Now use this information to figure the scale for this map in km/inch. |
Step 6. This is the final step! A) Convert the distances D to fit the scale on the map; fill in the last column, Scaled Distance for Map, in the table with these data. B) Use the distances you computed in the table for U and the scale for the map to draw a circle with center at each station and radius the scaled distance from that station to the epicenter. C) Look at these circles and locate the epicenter. D) What are the coordinates of the epicenter? What city or town is it near? |
Note: P- and S-wave travel is actually non-linear. For simplicity, we use a linear approximation in this study. |
Follow-up Steps
|
This material is based upon work supported by the National Science Foundation under Grant GEO-0355224. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.