Keyah Math Study 4, Level 2
Mathematical Content : Circumference of a circle, geometry, volume of a sphere
Objective: Use the method of Eratosthenes to make an estimate of the circumference of the Earth using locations in Arizona; use this estimate to compute its radius and volume
Eratosthenes’ Measurement of the Circumference of the Earth in Arizona
Introduction
This set of exercises gives you the opportunity to use the methods of Eratosthenes locally ( Arizona) to estimate the circumference of the Earth. It is slightly different in that the locations we use are farther north than the ones Eratosthenes used, so the angles are different. We suppose the measurements here are taken at noon on the fall equinox, this is when the sun is directly above the equator on its path from summer to winter in the Northern Hemisphere.
We use Kaibito and Superior as the two locations instead of Syrene and Alexandria. Kaibito is a small village on the Navajo Reservation in northern Arizona, almost due north of Superior, this will be one of the stations we use to complete these calculations. The other station is Superior, Arizona, a copper mining town about 60 miles east of Phoenix.
Using Math to Solve the Problem
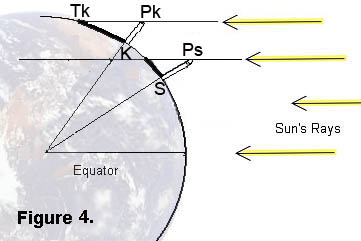
Vertical poles are erected at both stations and angles are measured similar to the way they were measured in by Eratosthenes.
S = the base of the pole in Superior, AZ;
TS = the tip of the shadow cast by the pole in Superior; TK = the tip of the pole's shadow in Kaibito; PS = the top of the pole in Superior; PK = the top of the pole in Kaibito; E = the center of the Earth. |
The measurements give these values:
Angle SPSTS = 33.3o (try to measure this yourself on the next equinox);
Angle SPKTK = 36.6o.
The direct distance from Superior to Kaibito is 367 km.
Notation: Some formulas you’ll need Circumference of a Circle: C = 2 πr Volume of a Sphere: V = (4/3)πr3 r = radius of sphere |
Question 1: What is the circumference of the Earth?
|
Question 2: What is the radius of the Earth?
|
Question 3: What is the volume of the Earth?
|
Here are some follow-up exercises:
Look at a topographical map of New Mexico or Arizona and choose two locations to use to measure the circumference of the Earth. You’ll need to know the latitudes and longitudes of your chosen locations in order to find the angles, and the places must be on approximately the same longitude (why?). You can also use the internet to find this information, go to www.topozone.com. Don’t choose places too close together because this will decrease your accuracy. You’ll need to estimate the direct distance between the locations—use the map scale or find it on the internet. There are other variations on this exercise, for example, you can change the time of year, maybe to a solstice. You’ll need the fact that the Earth’s axis is tilted 23.5 o to the plane of the solar system. Or you can change the location to your favorite region of the World. |