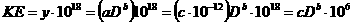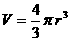Keyah Math Module 13, Level 4
Mathematical Content : Circumference of a circle, geometry, volume of a sphere
 Impact Processes: Meteor Crater, Arizona
Impact Processes: Meteor Crater, Arizona
What was the size of the meteorite that formed Meteor Crater?
Warm-up Questions
-
Have you ever seen a crater that was formed by a meteor impact?
-
After looking a pictures of Meteor Crater, how wide and how deep do you think it is?
-
How big would the meteor have been to form this size crater?
-
How fast would it have been travelling?
Understand the Problem:
A meteor falling toward the Earth is propelled by gravitational attraction. Because it is moving, the meteorite has an energy of movement or kinetic energy (KE), which is described by the equation:
|
If the meteorite is accelerating downward, its KE must be increasing as the square of the velocity! If the meteorite is big enough, it will pass through the atmosphere without burning up completely. When it strikes the surface of the Earth, its velocity and KE go to zero in an instant, but the law of conservation of energy holds that the energy is not simply lost; it is transferred to the surroundings as heat, light, and work, sending out shock waves and excavating a crater far larger than the meteorite itself.
Consider the factors that would determine how “large” a crater is formed. In part, this would depend on geological conditions specific to the impact site, such as the mechanical properties of soils and rocks. However, one might also assume that KE of the meteorite is a more important factor: the more energy delivered upon impact, the “bigger” the crater that is excavated. (We will use diameter to represent crater “size,” because as a crater is eroded away through time, its diameter changes far less than its depth.)
If KE is the most important (controlling) factor, and we can find a mathematical relationship between KE and crater diameter, we can take the dimensions of Meteor Crater and calculate the KE, and then the mass, of the offending meteorite. From the mass, we can then calculate the "size" (more precisely the volume) of the meteorite, because volume and mass are related by density, and we have actual fragments of the meteorite on which density has been measured.
Gather Data:
What data are available to help us solve this problem?
The impact that formed Meteor Crater is beyond history; evidence suggests that it occurred about 50,000 years ago. An impact of this size has not been observed on Earth in recorded time (and most would likely consider that a good thing!). But in the last century, for better or for worse, human beings have devised and experimented with a process of comparable destructive power: nuclear explosions. Until the advent of treaties restricting the practice, nations tested nuclear weapons by detonating them at or just beneath the surface.


Sedan, NV nuclear testing explosion and resulting crater. Image source http://rst.gsfc.nasa.gov/
In the United States, most nuclear weapons testing took place at the Nevada Test Site, in the Mojave and Great Basin Deserts of south-central Nevada, on the homelands of the Newe (Western Shoshone) people. The Newe had no say in the testing, and continue to work for restoration of these lands.
Nuclear explosions often excavated craters identical to those attributed to meteorite impacts. TheKE released in these blasts was known to the weapons designers, so here was a relationship between energy and crater size. This information was eventually made public, and planetary geoscientists made use of this relationship to estimate the KE needed to excavate impact craters of various sizes and ages, on Earth and other planets.
Some of these data, for what are thought to be actual meteorite impact craters are tabulated here. Crater diameter is reported in meters (m) and KE in joules (J).
Crater |
Diameter(m) |
Kinetic Energy of Impact (J) x 1018 |
3800 |
2.461 |
|
12000 |
15.85 |
|
23000 |
310 |
|
32000 |
1000 |
|
70000 |
14500 |
|
140000 |
205000 |
Source: Roddy: Dence et al., 1977.
We can use mathematical regression on these data to derive an equation relating these two variables:
Notation KE = kinetic energy (in J) released by the impact of the meteorite D = diameter (in meters) of the resulting crater |
This will enable us to calculate KE of impact for any Earth crater of known diameter, such as Meteor Crater. However, our ultimate target (so to speak!) is the volume of the meteorite, and for that we will need two more equations:
Information: This equation models kinetic energy, |
Information This equation models density, |
Solve the Problem:
Use the online applets or your calculators to answer the questions below.
Problem 1: Make points from the data provided in the table: the first coordinate should be the diameter of the crater and the second coordinate should be the kinetic energy. Write the second coordinate as shown in the table, just remember that the real value for KE must be multiplied by 1018. Use the power regression applet. |
Problem 2: Use power regression to find the equation of best fit. Round constants to 3 decimal places. |
Information and Notation: The equation as given by the power regression applet has the general form |
We will use this equation for craters with diameters between 500 and 140,000 meters, 500 < D < 140,000.
Information: Meteor Crater is about 1,200 meters in diameter. |
Problem 3: Now you are ready to determine the size of the meteorite that formed Meteor Crater.
Assume The meteorite was approximately spherical as it plunged to Earth. |
Information You can find its radius using the equation for the volume of a sphere, where V = volume of the meteorite in cubic meters (meters3) |
Follow-up Questions
|
This material is based upon work supported by the National Science Foundation under Grant GEO-0355224. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.

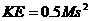 where M is the mass of the meteorite and s is its velocity.
where M is the mass of the meteorite and s is its velocity. 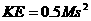
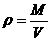
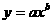
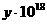 represents KE, the kinetic energy in Joules (J), and
represents KE, the kinetic energy in Joules (J), and 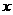 represents D, the diameter of the crater in meters
represents D, the diameter of the crater in meters .
. 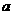 ' and '
' and ' ' are constants determined by the regression of the data. The coefficient '
' are constants determined by the regression of the data. The coefficient '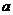 ' should be in scientific notation. In this case,
' should be in scientific notation. In this case,  with c in the form x.xxx).
with c in the form x.xxx).