Keyah Math Module 2, Level 2
Mathematical Content : Basic algebra, solving equations
 Volcanic Processes:
Volcanic Processes:
Sunset Crater, AZ
Objective: The velocity of bombs ejected from the crater during its eruption is determined using given equations.
Introduction
Sunset Crater is located about 15 miles (25 kilometers) northeast of Flagstaff, Arizona (see map below), along the east edge of the San Francisco volcanic field. Volcanic activity in this area was initiated about 6 million years ago and ended about 1000 years ago with the eruption of Sunset Crater (Reynolds et al., 1986; Holm and Moore, 1987; Duffield, 1997. Early eruptions were dominated by the construction of a composite volcano and related domes and flows while later eruptive phases were mostly eruptions of basaltic magmas that formed cinder cones and associated lava flows and spatter cones. More than 600 of these cinder cones have been documented in this region (Duffield, 1997) with Sunset and SP Craters being several of the more well know cones.
Initial eruptions at Sunset Crater ejected volcanic material ranging from fine ash to the size of watermelons (bombs); materials ejected during an eruption are referred to as tephra. Erupted bombs associated with this event were formed when sticky blobs of magma were ejected from the vent by gas-charged eruptions. As the hot and sticky masses spun in the air they took on different shapes and forms, some resembling footballs. These eruptions produced a mantle of loose, black material that accumulated around the central vent constructing a nearly symmetrical cone about 1,000 feet (300 meters) high and 1 mile (1.6 kilometers) in base diameter with a 400-foot-deep crater. All of the erupted material associated with this event may have blanketed more than 800 square miles, but presently about 122 square miles are covered with erupted tephra (Holm and Moore, 1987).
As part of the formation of the Sunset Crater cinder cone, basaltic lava flows (Bonito lava flow and Kana-a flow) erupted along cracks and fissures at the base of Sunset Crater. The Bonito lava flow traveled to the north-northwest for around 3,700 feet (1,130 meters) whereas the Kana-a flow migrated from the east of the cone northeast for about 4 miles (6.4 kilometers). Holm and Moore (1987) also describe small cones to the southeast of the main cinder cone.
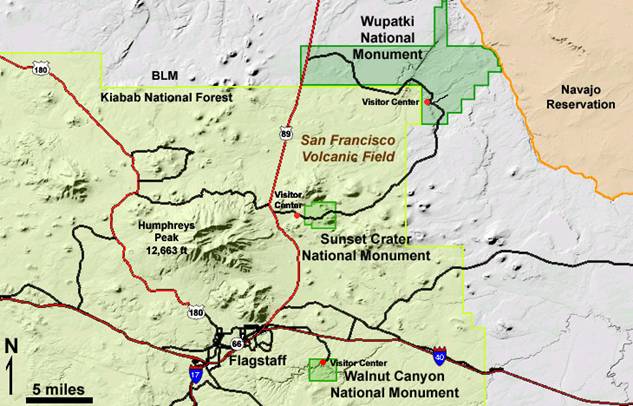
A shaded relief computer image of Sunset Crater and other features in the area image from the United States Geological Survey;

Sunset Crater as viewed to the south. Note the lava flows and other cinder cones in the field (http://www.nps.gov/sucr/naturescience/volcanoes.htm).

View of Sunset Crater from the west near Sugarloaf Mountain. Photo was taken by David Gonzales
Warm-up Questions
1. How fast do you think a bomb ejected from the Sunset eruption would travel?
2. How far?
3. Would it travel as fast as a Ferrari? A bullet? A shooting star?
4. How much damage would it do to your car if an ejected bomb hit it?
Using math to find the velocity of bombs ejected from the Sunset eruption
Sunset Crater cone dimensions: The Sunset eruption is unusual because the volume of volcanic products (about 0.7 cubic miles, 3 cubic km) is large for a Strombolian event, the air fall dispersal was large, and the discharge rate for magma was high. Strombolian eruptions are relatively low-level volcanic eruptions, named after the Italian volcano named Stromboli, where such eruptions consist of ejection of tephra to altitudes of tens to hundreds of meters. They are small to medium in volume, with sporadic violence.
In the last eruption of Sunset Crater in 1064 and 1065 A.D. (Duffield, 1997), fragments of volcanic rock and erupted magma were ejected into the area surrounding the cone.
Before you being this exercise, it might be useful to visit the Visual Exercises and Component using Stromboli program at:
http://www.swisseduc.ch/stromboli/volcano/simulation/index-en.html
The goal of this study is to estimate the initial and terminal velocity of large volcanic bombs ejected from Sunset Crater.
Information and Assumptions
-
Sunset Crater cone dimensions: the cone is about 1,000 feet (300 m) high and 1 mile (1.6 km) in base diameter
-
Angle of ejection: α = 45 degrees
-
The maximum distance that large volcanic bombs travel is 800 meters.
Notation:
The formulas below are only valid when the angle of ejection α = 45 degrees |
Formula 1 The height (in meters) at time t is |
Formula 2 The horizontal distance at time t is |
Formula 3 The velocity at time t is |
Problem: To find tmax , the maximum time a bomb travels, v0, the initial velocity of the bomb, and V, the total velocity at impact
Question 1: What is the initial velocity? To answer this, follow the steps below. Use meters for height and distance. A) What is the height and the distance when the volcanic bombs hit the ground? (These are the values of z and u when t = tmax) B) Re-write formula 1 for z by substituting z0= 300 and C) Use formula 2 and your answer to step A to write an equation for tmax in terms of v0. D) Substitute your answers from steps A, B, and C in the equation for z when t = tmax and solve for v0. |
Question 2: What is tmax? (Use formula 2.) |
Question 3: What is V, the total velocity at impact? (Use formula 3.) |
Question 4: Steve builds a summer home just outside of Flagstaff, but only 2000 meters from Sunset Crater. Suppose there is another eruption from the crater. What will the initial velocity of a bomb need to be to destroy Steve’s new vacation home? |
Follow-up Questions
|
This material is based upon work supported by the National Science Foundation under Grant GEO-0355224. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.

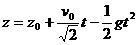 and
and 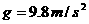 .
.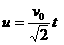 .
.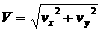 , where
, where 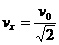 and
and 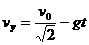 .
.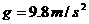 .
.