KÉYAH MATH HOME

TOPIC MENU

MODULE MAP

TOPIC MAP

MATH TOOL CHEST

APPLET INSTRUCTION

INSTRUCTOR RESOURCES

CONTACT

Keyah Math Study 11, Level 3

Mathematical Content: of a circle, geometry, volume of a sphere, basic algebra, formulae for gravitational attraction

Size, Mass and Density of the Earth:

This study has two parts. In the first part you will estimated the circumference, radius and volume of the Earth.  In the second part you will determine the mass and density of the Earth.  This module combines the material from KM#4 and KM#9

Part 1: Estimating the Circumference of the Earth

The goal of this study is to learn how Eratosthenes made the first close estimate of the circumference of the Earth and then use his estimate to compute its radius and volume.

Warm up question:
Without leaving this country, how could you figure out how far it is all the way around the World?

Introduction
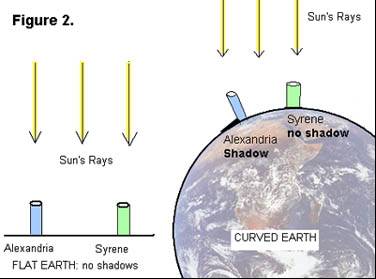
Around 250 BC, at noon on the day of the summer solstice (when the sun is at its highest point in the Northern Hemisphere) in Syrene, Egypt, sunlight filled the vertical shaft of a well; this indicates that the sun is directly overhead, so a vertical pole would cast no shadow. Eratosthenes, who lived in Alexandria, heard of this from a traveler. So on the same day, different year, he noticed that in Alexandria, some 800 kilometers (km) away, a vertical pole cast a shadow. From these observations, he made two deductions:

A. the earth is curved;

B. found the first estimate for the circumference of the Earth.

The Earth is Spherical
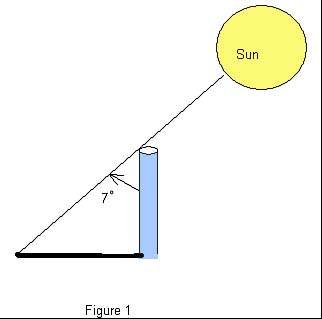
He measured the angle made by the pole and a line joining the tip of the shadow and the top of the pole (see Figure 1) and found the angle to be about 7^o. Then he assumed that light rays from the sun to the Earth were essentially parallel since the sun was so far away and the Earth was so small relative to the sun. From this, and his observations in Alexandria and Syrene, he concluded that the Earth must be curved (see Figure 2), and therefore must be spherical.

Using Math to Find the Circumference of the Earth
Next, he used all this information to obtain the first nearly accurate estimation of the circumference of the Earth. Here’s how:

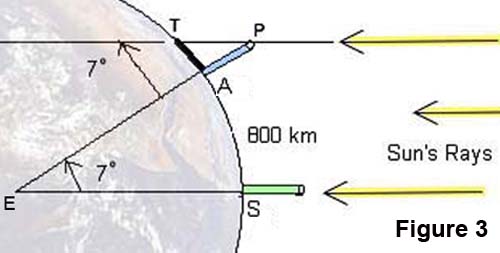
In the (not-to-scale) Figure 3:
A denotes the base of the pole in Alexandria;
S the base of a pole in Syrene;
T the tip of the shadow cast by the pole in Alexandria;
P the top of the same pole;
E the center of the Earth.
Angle APT was measured to be 7^o, so by Euclidean geometry interior angles 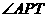 and 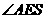 are equal, thus angle .
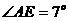There are 360o in a complete circle, so the portion of the circumference of the Earth between A and S is
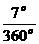, which is approximately  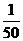(or, 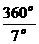 is approximately 50).
The distance from Alexandria to Syrene is 800 km, so he concluded that the circumference of the Earth must be

!

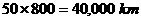This estimate is very close to modern accurate measurements, so Eratosthenes gets credit for the first calculation of the size of the Earth.
We can get a slightly different answer if we compute more accurately: 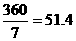, so if we multiply

Notation: Some formulas you’ll need (r = radius of circle / sphere) Circumference of a Circle: C = Volume of a Sphere:

Part 2: Determining the Mass and Density of the Earth

The goal of this study is to learn how the famous physicist, Sir Isaac Newton, computed the mass of the Earth, and then use this to compute its density.
Basic Concepts

• Any object in the Universe attracts any other object.  

• The force that moves objects toward each other is called gravity.

• The mass of an object is a fundamental property of the object with measured in kilograms (kg).

• Even though we often use weight and mass interchangeably in everyday language, the weight of an object depends on the force of gravity. If you went to the moon, your mass would not change but your weight would be much less. The weight of an object is the force of gravity on the object; this can be described by the equation

w = mg where m is the mass of the object and g is the acceleration due to gravity.

• The density of an object is the mass per unit volume.

In the year 1680, Sir Isaac Newton discovered the famous equation known as the Law of Gravitational Attraction on two objects. You will use this result, together with another result also due to Newton, to compute the mass of the Earth.

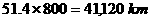
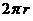
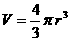
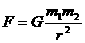Notation: Newton ’s Law of Gravitational Attraction, , describes the force with which two objects attract each other. 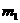G is called the universal gravitational constant and its value is known  and 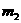 denote the masses of the two objects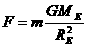 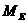r is the distance between the objects. For an object with mass m on the surface of the earth, this equation becomes Equation 1: where  is the mass of the earth and  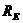is the radius of the earth. 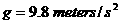Newton’s Second Law of Motion, F = mass x acceleration describes the relationship between force, mass and acceleration. On the surface of the earth the acceleration of gravity is about   and we have 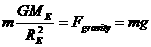Equation 2: F = mg. Since equations 1 and 2  describes the same force, we have ,which simplifies to our basic equation Basic Equation: .

Thought questions

• If the distance between two objects increases does the force of attraction increase or decrease?

• Which object will have greater acceleration due to gravity, one of very large mass or one of very small mass?

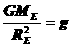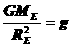You will use the basic equation to estimate the mass, volume and density of the earth.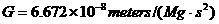

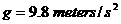
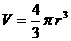
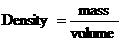
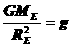The answers to the following questions will use Newton’s methods to determine the mass and density of the Earth

Here are some follow-up questions to think about:

• Click here for the answers

This material is based upon work supported by the National Science Foundation under Grant GEO-0355224. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.